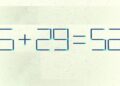Mesmo os estudantes apaixonados por matemática podem ficar surpresos quando tiverem contato com a matéria de Cálculo no ensino superior.
Diversos exercícios matemáticos, como: limites, funções, derivadas e integrais, podem apresentar complexidades. No entanto, em alguns casos, o aluno pode se deparar com conceitos que simplesmente “não existem”.
Parece impossível, mas saiba que isso pode acontecer. No estudo sobre limites de funções reais, por exemplo, o resultado de um problema pode mostrar que se os limites laterais não forem iguais, o limite não existe.
E é nesse momento que o aluno pode se questionar, “mas por que eu preciso aprender isso?”.
O professor de Física, Danilo Fróes, explica que “o estudo sobre limites é a base para todo o aprendizado da disciplina de Cálculo”. Portanto, o conteúdo é a porta de entrada para os outros conceitos que serão apresentados posteriormente.
Vale destacar que ao estudar limites, o estudante desenvolve o raciocínio matemático, afinal, eles devem ser utilizados quando uma conta não pode ser realizada na calculadora e o exercício é indeterminado. Por isso, o cálculo é feito por aproximação.
Saiba como começar a estudar limites
O conceito de limite é usado para demonstrar o comportamento de uma função nos momentos de aproximação de determinados valores na matemática.
De acordo com o portal Responde Aí, “às vezes, nos deparamos com funções que têm restrições ou que não são definidas em determinados pontos. Para conseguir estudar o que acontece com a função quando nos aproximamos desses pontos indefinidos, usamos o limite”.
O conteúdo é enorme e tem suas complexidades, por isso, os especialistas indicam criar um guia de estudos para melhorar e absorver o aprendizado.
A plataforma sugere a divisão em cinco temas:
- Introdução aos limites,
- Como sair de indeterminações,
- Limites fundamentais,
- Continuidade e assíntotas.
Os especialistas orientam que o estudo seja iniciado pelos conceitos introdutórios sobre limites, propriedades, limites laterais e existência do limite.
Na segunda parte, o estudante irá dedicar tempo aprendendo a resolver limites com indeterminações, através de alguns casos e métodos como:
- Quociente de polinômios com x tendendo a constante ou ao infinito,
- Conjugado,
- Infinito menos infinito,
- Teorema do confronto.
Na terceira fase do estudo, será estudado os limites fundamentais trigonométrico e exponencial. Ao fim dessa etapa, o aluno aprenderá sobre continuidade, Teorema do Valor Intermediário e extensão contínua.
Por fim, o estudo sobre limites na quinta parte deverá abranger assíntota horizontal, vertical e oblíqua.
“O segredo é ter um guia, que diga não só que tópicos estudar e em que ordem, mas que indiquem bons resumos e exercícios selecionados em ordem de dificuldade, com resolução passo a passo”, orienta a Responde Aí.
E então, gostou da matéria? Não deixe de ler também – ENEM: descubra o que mais cai na prova de Matemática.